Machine learning-based applications have become prevalent across consumer, medical, and automotive markets. Still, the underlying architecture(s) and implementations are evolving rapidly, to best fit the throughput, latency, and power efficiency requirements of an ever increasing application space. Although ML is often associated with the unique nature of (many parallel) compute engines in GPU hardware, the opportunities for ML designs extend to cost-sensitive, low-power markets. The implementation of an ML inference engine on an SoC is a great fit for these applications – this article (very briefly) reviews ML basics, and then highlights what the embedded FPGA team at Flex Logix is pursuing in this area.
Introduction
Machine learning refers to the capability of an electronic system to:
[LIST=1]
- receive an existing dataset of input values (“features”) and corresponding output responses
- develop an algorithm to compute the output responses with low error (“training”) and,
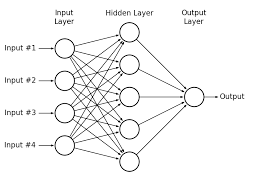
- deploy that algorithm to accept new inputs and calculate new outputs, with comparable accuracy to the training dataset (“inference”)The common hardware implementation of the ML algorithm is a neural network – loosely based on our understanding of the electrochemical interactions in the brain among a neuron cell nucleus, its dendrites, and the axons/synapses sending electrical impulses from other neurons to the dendrites. The figure below illustrates a “fully-connected, feed-forward” neural network, a set of nodes comprising:
- an input layer (the “features” of the data)
- additional computation layers (zero or more “hidden” layers)
- an output layer
In the fully-connected (acyclic graph) architecture, the computed value at the output of each node is an input to all nodes in the next layer.
An expanded view of each network node is shown in the figure below. The computed input values each have an associated multiplicative “weight” factor. The node calculates the sum of the weighted inputs – in vector algebra terms, the “dot product”. A “bias” value may also be used in the summation, as part of the node calculation.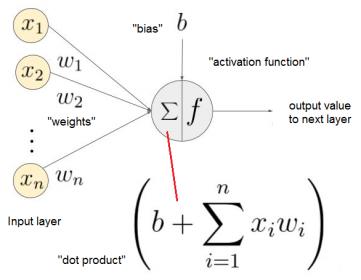
There are two importance (interrelated) characteristics of note in the neural network – “normalization” and “activation”. The numerical range of individual input features could vary widely – for example, one input could range from (-10,10), while another spans (0,1). The neural network designer needs to assess the relative importance of each feature, and decide to what extent the range should be normalized in the input layer. Similarly, this architectural decision extends to the activation function within the node, as part of the output calculation. A variety of (linear and non-linear) activation functions are in common use – a few examples are shown below, including functions that normalize the output to a specific range (e.g., (0,1), (-1,1)).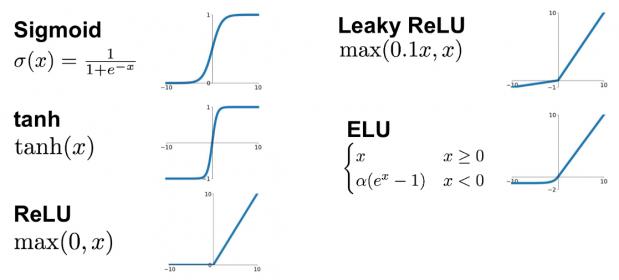
Some activation functions include a “threshold”, such that the output is truncated (to zero) if the dot product result is below the threshold value. (The axon and endpoint synapses that connect a neuron output to the dendrites of other neurons are also capable of complex electrical filtering – the brain is indeed a very unique system.)At the output layer, the activation function is a fundamental aspect of the neural network design. The desired output result could be a numeric value, or could be “classified” into (two or more) “labels”. The simplest classification would be a binary 0/1 (pass or fail, match or no_match), based upon comparisons to the threshold ranges defining each label.
Training/Test and Inference
The selected neural net architecture needs to be “trained”. A subset of the given input dataset records is selected, and feature values applied using the existing weights and biases at each node. The network output values are compared to the corresponding “known” output values for each input record. An error measure is calculated, which serves as the optimization target. Any of a number of error models can be used – two common examples are depicted in the figure below.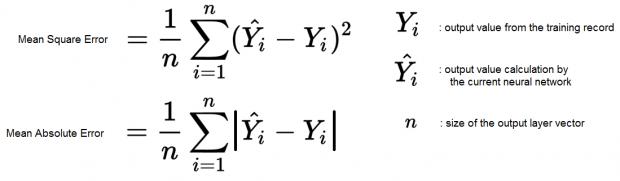
The training phase then adjusts the network weights and biases, re-submits the input training dataset, and re-calculates the error. Sophisticated algorithms are used during optimization to derive the (multi-dimensional) “surface gradient” of the error as a function of the weights and biases, typically working backwards from the output layer. The training phase iterates through multiple input data applications, error calculations, and weight/bias adjustments, until an error minimum is reached. Special techniques are employed to avoid stopping on a “local minimum” of the error response.Once the training phase completes, the remaining dataset records serve as a separate “test” sample. These test records are applied to the network with the final training weights/biases, and an “accuracy” measure derived. (Accuracy is perhaps best understood for classification-based outputs – did each classified result for each test record match the given label? Also, considerable ML research is being pursued to select “good” training/test subsets, as well as identify “noisy” input data that may not be representative of the final environment.)
Once a neural network with suitable accuracy has been derived, the design implementation is ready to be deployed as an “inference engine” for general purpose use.
Numeric Resolution
A key finding from ongoing ML research relates to the resolution of the weights, bias values, and activation calculations. During the training phase, high resolution calculations are needed at all layers – e.g., 32-bit floating point (fp32). However, once the network is ready to use for inference calculations, a reduction in resolution may result is minimal loss in accuracy, with corresponding improvements in power/area/cost. For example, weights and biases could be transformed to fp16 or 8-bit fixed point representations at some/all layers of the network, while maintaining comparable accuracy (link) – that is a game-changer.ML and Flex Logix eFPGA tiles
I had an opportunity to chat with Geoff Tate and Cheng Wang at Flex Logix about their initiatives into supporting inference engines within an embedded FPGA implementation.Cheng indicated, “As you may recall, our eFPGA designs utilize modular, abutted tiles, allowing customers to build the IP in the capacity and configuration best suited for their application. In addition to the logic-centric tile (comprised of programmable LUT’s), we offer a DSP-centric tile with a rich mix of multiply-accumulate functions. ML customers are seeking high MAC density, optimal throughput, and power efficiency – we have prepared an ML-centric tilewith a concentration of programmable int8 MAC’s, ideally suited for many ML applications.” (This ML tile is similar to, yet simpler than, the DSP offering. Like the DSL tile, it can be readily incorporated into a larger eFPGA block. Also, the MAC’s can be configured as 8×16, 16×8, and 16×16.)

Cheng continued, “We are engaging with customers seeking a variety of network options – e.g., even smaller bit resolutions, unique memory interfacing for faster access to retrieving weights and biases.”
An increasing area of ML development relates to network partitioning. For architectures larger than the physical implementation, a set of successive, partial calculations are needed, with partition weights/biases updated prior to each evaluation. The overall throughput is thus a strong function of the time to load new weights and biases. The figure below illustrates how block partitioning applies to matrix multiplication (from linear algebra).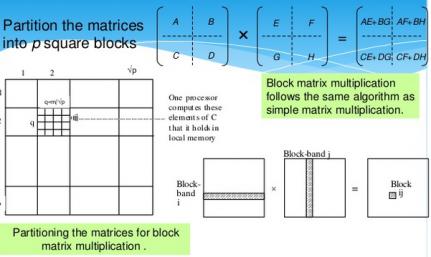
For ML implementations targeting IoT edge devices (with input patterns representing sensor data), network partitioning may involve dividing the overall calculation between edge and host. In these cases, a detailed tradeoff assessment is made between throughput and power efficiency/cost.Geoff added,“Many customers are seeking an embedded FPGA solution with an ML-optimized MAC resolution. Our implementation style enables us to offer a tailored solution for a specific process and architecture within 6-8 months. Also, we realize there are a number of ML coding libraries used to define the neural network architecture – e.g., Caffe, TensorFlow. (link – also, see Footnote) A software toolset to establish a flow from the ML code to our eFLX compiler can be made available.”
The attractiveness of a high throughput, power-efficient, and low cost embedded SoC inference engine implementation using an eFPGA optimized for the specific resolution requirements will no doubt greatly expand the breadth of ML applications. For more information on the Flex Logix ML tile specifications, please follow this link.
–chipguy
Footnote: The link provided is a YouTube video of a Stanford University CS lecture describing Caffe and (especially) TensorFlow ML software libraries. The most popular class in many CS departments is no longer “Introduction to Object-Oriented Programming”, but rather “Introduction to Machine Learning”. 😀
PS. This introductory description above depicted a full-connected, acyclic, two-dimensional neural network graph, with a set of one-dimensional vectors for weights and biases. ML research has also pursued many other complex network topologies than depicted above, include graphs with feedback connections between layers. Also, the training phase was “supervised”, in that output values/labels were assumed to be provided for each input record. Additionally, “unsupervised” training algorithms are used when the inputs do not include corresponding output data – this represents a significantly more complex facet to ML, as the “pre-training” phase attempts to identify (higher-level) features from correlations among the detailed (lower-level) inputs.






Comments
There are no comments yet.
You must register or log in to view/post comments.